Health Insurance Design and Consumer Behavior
Overview
So far, we’ve established that health insurance:
- improves financial stability and reduces financial risks of medical spending
- improves health, particularly for those with chronic conditions
Overview
But health insurance is also a complex product that is difficult to understand and evaluate. How can we expand access and adoption of health insurance?
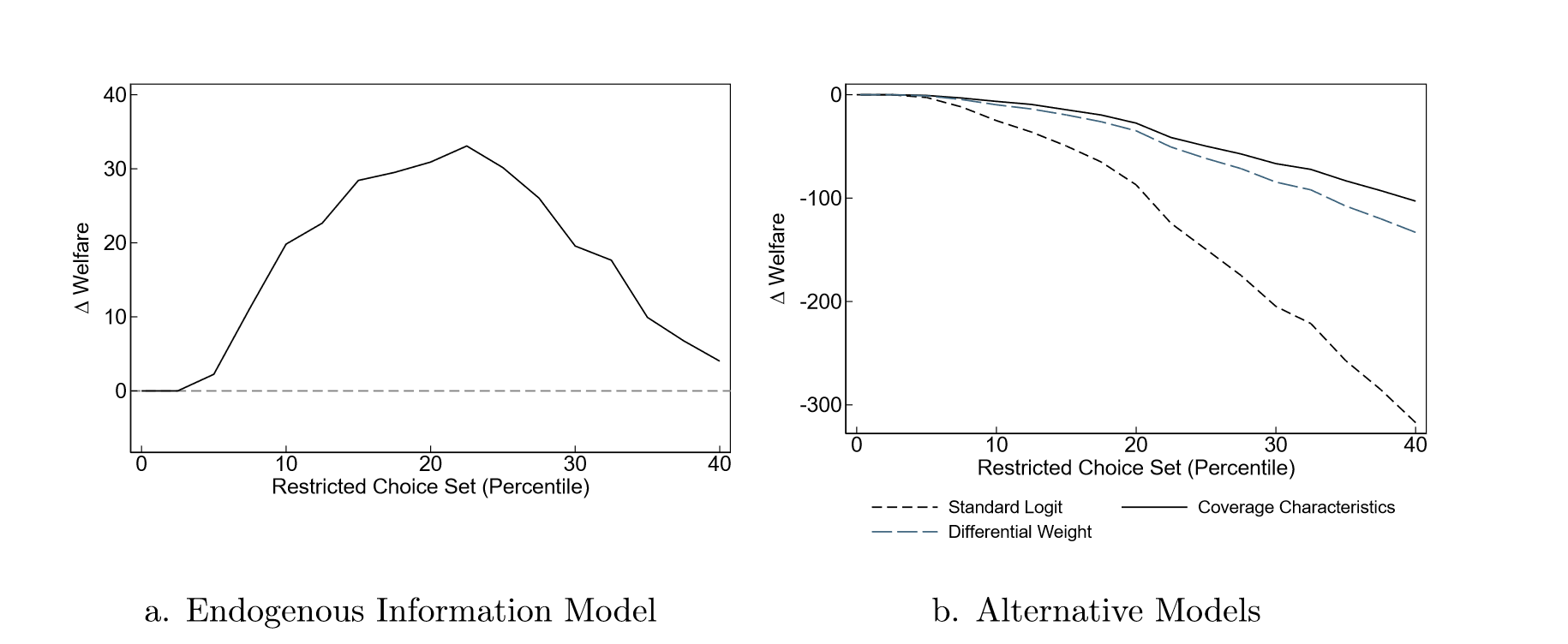
Endogenous Information and Simplifying Insurance Choice
(see Brown and Jeon (2023) for details)
Empirical motivation
- Individuals acquire more information when there are higher costs of a poor choice
- Invesitgate with Medicare Part D, which has a large number of plans and a complex choice environment
Economic model
- Structural model of health insurance choice with endogenous information acquisition
- Builds on framework of rational inattention in discrete choice
- Often computationally intractible, but authors offer a tractible approximation with feasible estimation
\[\begin{align*} u_{ij} &= \alpha v_{ij} + \beta x_{j}^{u} & + \alpha p_{j} + \theta x_{j}^{k} + \epsilon_{ij} \\ &= \xi_{ij} & + \alpha p_{j} + \theta x_{j}^{k} + \epsilon_{ij} \end{align*}\]
- Person \(i\) chooses among plans \(j \in J\)
- Plan \(j\) has known characteristics: price \(p_{j}\) and other things \(x_{j}^{k}\)
- Plan \(j\)j has (initially) unknown characteristics: price \(v_{ij}\) and other things \(x_{j}^{u}\)
- \(\xi_{ij}\) comes from multivariate CDF \(G_{i}(\xi_{i})\)
- Two-stage choice process: first choose how much information to acquire (denoted by signal, \(s_{i}\)), then choose plan
- Entropy-based cost function for information acquisition
- Constant marginal cost, \(\lambda\), with total costs:
\[\lambda (H(G_{i}) - E_{s_{i}}[ H(F_{i}(\xi_{i} | s_{i}))]),\]
- \(F_{i}(\cdot)\) is the posterior belief of \(\xi_{i}\) after acquiring signal \(s_{i}\)
- \(H(G)\) is entropy of prior belief \(G\) and \(H(F)\) is the entropy of posterior belief \(F\)
- Intuition: costs are proportional to reduction in entropy (or uncertainty) as measured by the relative information gained from the signals
An aside on Entropy
- Measure of uncertainty
- More informative than variance as entropy is sensitive to the shape of the distribution, not just its spread
- Uniform distirubtion has maximum entropy, while a point mass has minimum entropy
Matějka and McKay (2015)
In this setup, individuals act as if maximizing \(\tilde{u}_{ij}\), where
\[\tilde{u}_{ij} = u_{ij} + \lambda log P_{ij}^{0} + \lambda \varepsilon_{ij}\]
- \(u_{ij}\) is true utility
- \(P_{ij}^{0}\) is expected choice probability based only on priors, \(G\)
- \(\varepsilon_{ij}\) captures error in beliefs
- Brown and Jeon (2023) derive closed form expression for choice probabilities with stronger assumptions on \(G_{i}(\xi_{ij})\)$ and distribution of original error, \(M(\epsilon_{ij})\)
Preliminary evidence
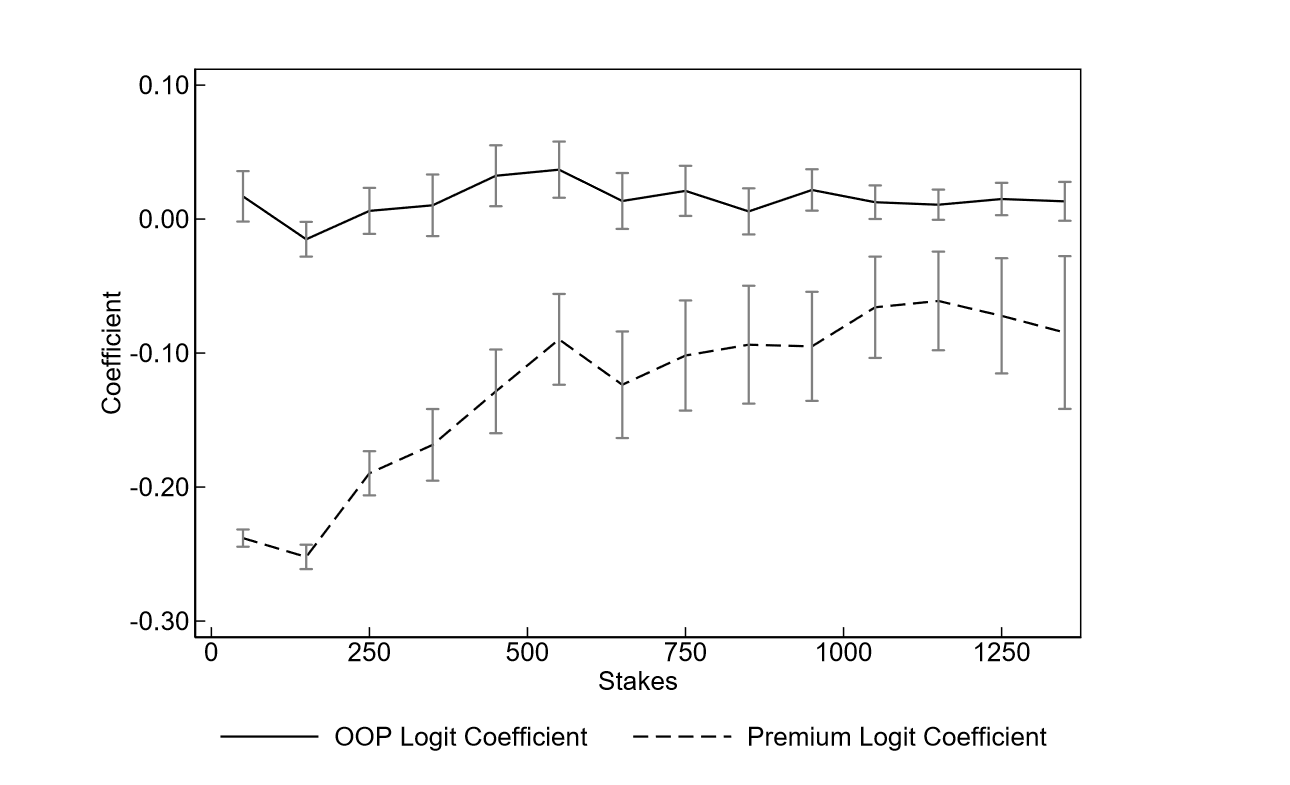
- Brown and Jeon (2023)
- ‘stakes’ measured as expeced out of pocket costs, \(v_{ij}\)
Main finding
Health Insurance Design and Consumer Behavior
(see Ho and Lee (2020) for details)
Motivation
- For a single insurance plan, how much cost sharing is optimal?
- How much can then be gained by introducing a menu of plan options?
- How sensitive is this to how enrollee selection across plans is managed?
- Can introducing plan differentiation along nonfinancial dimensions improve outcomes?
Setting and data
- Harvard Health Insurance Plans, 2014-2016
- Introduced cost-sharing in 2015 for all nonunion employees
- Re-introduced zero-deductible and zero-coinsurance plan in 2016
- Examine plan changes among uninon and nonunion employees as these choice sets changed
Model and estimation
- Two-stage model of plan choice and healthcare utilization
- Model allows for adverse selection in plan choice and moral hazard in utilization
Results 1: Optimal cost sharing
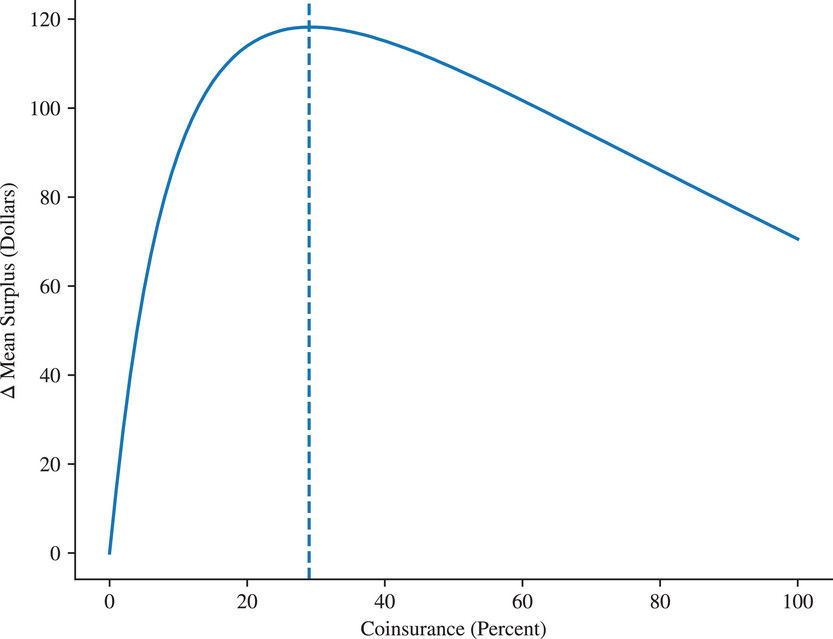
- Optimal cost sharing of 29% with zero deductible
- Large initial gains with even small cost sharing
Results 2: Multiple plan options
- Meaningful consumer surplus gains in two-plan environment (with optimal plan design) under plan assignment
- Gains erased when employees can self-select
- Nonfinancial differentiation can be more effective
Future research
“We conclude by identifying two promising avenues for future research.”
- There may be benefits from developing more finely tuned cost-sharing schemes, where OOP costs can vary depending on the individual’s diagnosis
- There is an open question of how many insurance carriers (as opposed to plans) an employer should offer as options to its employees.
- Induce more competition on premiums and fees
- Protect an employer from hold-up in future negotiations with insurers, particularly if there are large switching costs
- Downside: may limit insurers’ bargaining leverage with medical providers, making it harder for them to negotiate favorable medical rates
References
Brot-Goldberg, Zarek, Timothy Layton, Boris Vabson, and Adelina Yanyue Wang. 2023. “The Behavioral Foundations of Default Effects: Theory and Evidence from Medicare Part D.” American Economic Review 113 (10): 2718–58. https://doi.org/10.1257/aer.20210013.
Brown, Zach Y, and Jihye Jeon. 2023. “Endogenous Information and Simplifying Insurance Choice,” August. https://public-websites-umich-edu.proxy.library.emory.edu/~zachb/brown_jeon_endo_info.pdf.
Ho, Kate, and Robin S. Lee. 2020. “Health Insurance Menu Design for Large Employers,” Working Paper Series, September. https://doi.org/10.3386/w27868.
Matějka, Filip, and Alisdair McKay. 2015. “Rational Inattention to Discrete Choices: A New Foundation for the Multinomial Logit Model.” American Economic Review 105 (1): 272–98. https://doi.org/10.1257/aer.20130047.